Practice Test 2 - AP Physics 1 Premium 2024
Section I: Multiple-Choice
TIME: 90 MINUTES
50 QUESTIONS

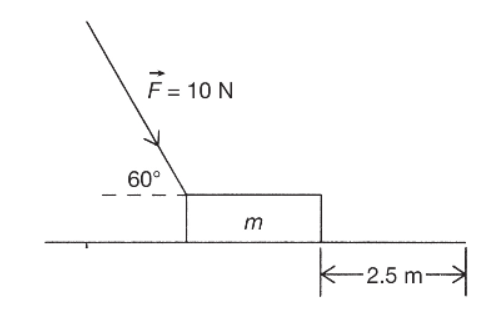
1. A block (m = 1.5 kg) is pushed along a frictionless surface for a distance of 2.5 meters, as shown above. How much work has been done if a force of 10 newtons makes an angle of 60 degrees with the horizontal?
(A) Zero
(B) 12.5 J
(C) 21.6 J
(D) 25 J
2. What is the instantaneous power due to the gravitational force acting on a 3-kilogram projectile the instant the projectile is traveling with a velocity of 10 meters per second at an angle of 30 degrees above the horizontal?
(A) 300 W
(B) 150 W
(C) −150 W
(D) −300 W
3. A hockey puck of an unknown mass is sliding along ice that can be considered frictionless with a velocity of 10 meters per second. The puck then crosses over onto a rough floor that has a coefficient of kinetic friction equal to 0.2. How far will the puck travel before friction stops it?
(A) 2.5 m
(B) 5 m
(C) 25 m
(D) Depends on the mass
4. A dart is placed onto a spring. The spring is stretched a distance x. By what factor must the spring’s elongation be changed so that the maximum kinetic energy given to the dart is doubled?
(A) 1/2
(B) 2
(C) 4
(D) 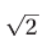
Questions 5 and 6 are based on the following information:
A 10-kilogram projectile is launched at a 60° angle to the ground, with a velocity of 200 m/s. Neglect air resistance. The ground is level.
5. Compare this projectile with a 5-kilogram projectile launched under the same conditions but at a 30° angle. The 5-kilogram projectile will
(A) go higher up and farther along the ground
(B) go equally high and equally far along the ground
(C) neither go as high nor as far along the ground
(D) not go as high but go equally far along the ground
6. As the launch angle is lowered to 45°, the maximum horizontal distance traveled by the projectile will
(A) decrease only
(B) increase only
(C) increase and then decrease
(D) decrease and then increase
__________________________________________________________________________________
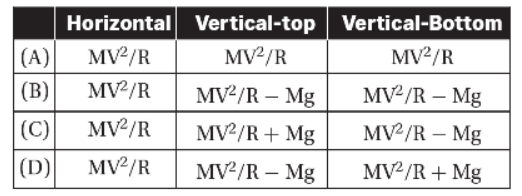
7. An object of mass m rests on top of a spring that has been compressed by x meters. The force constant for this spring is k. The mass is not attached to the spring and will shoot upward when the spring is uncompressed. When released, how high will the mass rise?
(A) mg − kx
(B) kx2/mg
(C) (kx2/2mg) − x
(D) (k/m)½x
8. Which of the following is the best method for finding a spring’s force constant k?
(A) Hanging a known mass on the spring and dividing the weight by the length of spring
(B) Hanging several known masses on the spring, taking the average value of the mass, and dividing by the average length of the spring
(C) Hanging several known masses on the spring and finding the area under the curve after plotting force versus extension
(D) Hanging several known masses on the spring and finding the slope of the graph after plotting force versus extension
9. How much of a braking force is applied to a 2,500-kilogram car on the Moon (g = 1.6 m/s2) that has an initial velocity of 30 meters per second if the car is brought to a stop in 15 seconds?
(A) 5,000 N
(B) 6,000 N
(C) 8,000 N
(D) 25,000 N
10. A 1-kilogram object is moving to the right with a velocity of 6 meters per second. It collides with and sticks to a 2-kilogram mass, which is also moving to the right, with a velocity of 3 meters per second. What happens to the total kinetic energy during this collision?
(A) The kinetic energy is conserved because the collision is elastic.
(B) The kinetic energy is conserved even though the collision is not elastic.
(C) Some kinetic energy is lost during the collision even though total momentum is conserved.
(D) Some kinetic energy is lost during the collision because of the elastic nature of the collision.
11. A ball with a mass of 0.2 kilogram strikes a wall with a velocity of 3 meters per second. It bounces straight back with a velocity of 1 meter per second. What was the magnitude of the impulse delivered to this ball?
(A) 0.2 kg · m/s
(B) 0.4 kg · m/s
(C) 0.6 kg · m/s
(D) 0.8 kg · m/s
12. Which of the following is an equivalent expression for the maximum velocity attained by a mass m oscillating horizontally along a frictionless surface? The mass is attached to a spring with a force constant k and has an amplitude of A.
(A) Ak/m
(B) A(k/m)½
(C) mg/kA
(D) A2k/m
13. A 0.5-kilogram mass is attached to a spring with a force constant of 50 newtons per meter. What is the total energy stored in the mass-spring system if the mass travels a distance of 8 cm in one cycle?
(A) 0.5 J
(B) 0.01 J
(C) 0.04 J
(D) 0.08 J
14. Which of the following expressions is equivalent to the magnitude of the escape velocity in terms of the magnitude of the orbital velocity v for a spacecraft?
(A) 2v
(B) v
(C) 4v
(D) 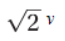
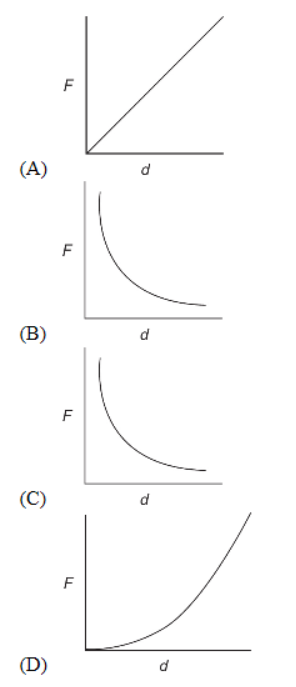
15. Which of the following graphs correctly shows the relationship between magnitude of gravitational force and distance between two masses?
16. Which of the following statements is true regarding why the net work done in lifting a book from the ground to the top of a shelf is zero?
(A) Air resistance (friction) took away any increase in kinetic energy.
(B) Gravitational potential energies are always negative.
(C) The force used to lift the book is a conservative force.
(D) The change in kinetic energy of the book is zero.
17. Which of the following best describes the forces present as a brick is sliding along the horizontal ground and coming to a halt?
(A) The net force is equal to the force of friction.
(B) The inertia of brick is supplied by the original push that got the brick moving.
(C) The forces on the brick are in equilibrium.
(D) The brick is pushing on the air in front of it harder than the air is pushing back on the brick.
18. A projectile is launched at a 30° angle to the ground with a velocity of 200 m/s. What is its speed at its maximum height?
(A) 9.8 m/s
(B) 100 m/s
(C) 173 m/s
(D) 200 m/s
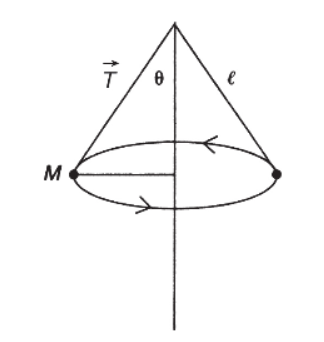
19. A conical pendulum consists of a mass m attached to a light string of length L. The mass swings around in a horizontal circle, making an angle θ with the vertical as shown above. What is the magnitude of tension, T, in the string?
(A) mg/cos θ
(B) mg cos θ
(C) mg/sin θ
(D) mg sin θ
20. The magnitude of the one-dimensional momentum of a 2-kilogram particle obeys the relationship p = 2t + 3. What was the velocity of the particle at t = 1 second?
(A) 5 m/s
(B) 2 m/s
(C) 1 m/s
(D) 2.5 m/s.
21. An object is experiencing a nonzero net force. Which of the following statements is most accurate?
(A) The linear and angular momentums of the object are both definitely changing.
(B) Although the linear momentum of the object is definitely changing, the angular momentum may not be.
(C) Although the angular momentum of the object is definitely changing, the linear momentum may not be.
(D) Neither the linear momentum nor the angular momentum is definitely changing.
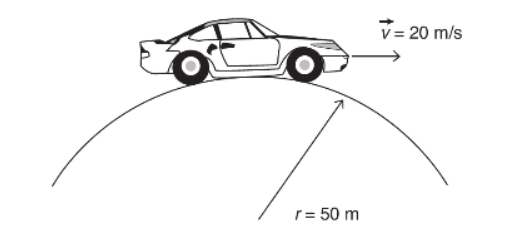
22. A car with a 500-newton driver goes over a hill that has a radius of 50 meters as shown above. The velocity of the car is 20 meters per second. What are the approximate force and the direction that the car exerts on the driver?
(A) 900 N, up
(B) 400 N, down
(C) 100 N, up
(D) 500 N, up
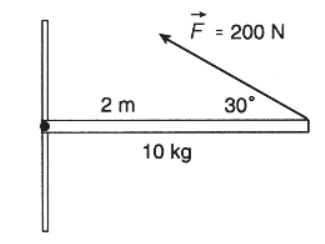
23. What is the net torque acting on the pivot supporting a stationary 10-kilogram beam 2 meters long as shown above?
(A) 198 N · m
(B) −198 N · m
(C) −102 N · m
(D) 102 N · m
Use the graph below to answer the following four questions (24–27):
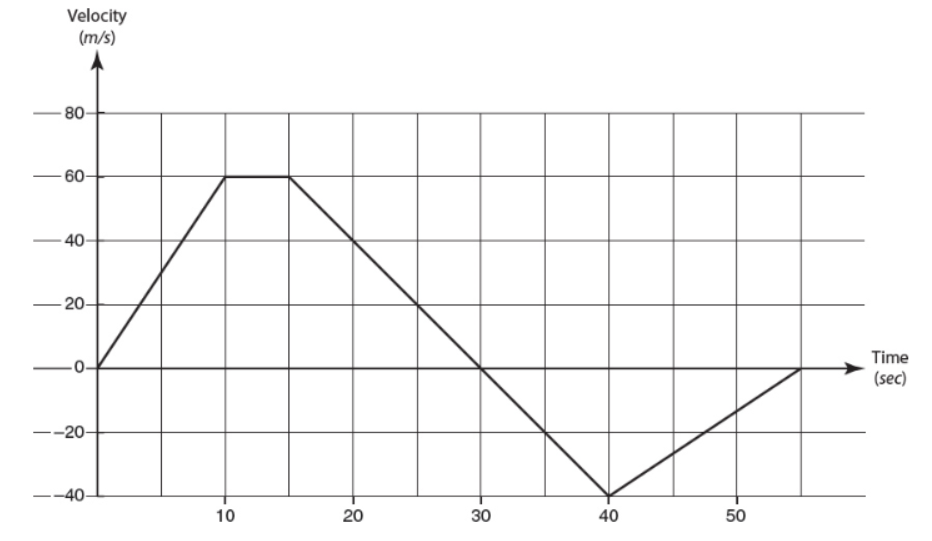
24. Which of the following statements best describes the acceleration over the 55 second of time graphed above?
(A) Increasing, constant, decreasing, increasing
(B) Positive, zero, negative, positive
(C) Positive until the 30 second mark, then negative for the rest of the trip
(D) The net acceleration is approximately 500 m/s/s for the entire trip.
25. What is the average acceleration for the 55 seconds of the graph?
(A) Approximately 500/55 m/s/s
(B) Approximately 5/4 m/s/s
(C) Approximately −100/25 m/s/s
(D) Approximately 0 m/s/s
26. How far does the car travel over the 55 seconds of the graph?
(A) 1550 m
(B) 550 m
(C) 0 m
(D) Cannot be determined
27. What is the instantaneous acceleration at the 40 second mark?
(A) 0 m/s/s
(B) −4/3 m/s/s
(C) −10/3 m/s/s
(D) −4 m/s/s
__________________________________________________________________
28. An old record player could bring a disk up to its 45 RPM speed in less than a second. If the same size disk can also be brought up to a speed of 75 RPM in about the same amount of time on another player, compare the two torques.
(A) The torques would be the same as the moment of inertia of the two disks are the same.
(B) The torques would be the same because of the conservation of angular momentum.
(C) The torque would be larger in the second case as it requires a greater angular acceleration.
(D) The torque would be larger in the second case as it entails both a larger force and a larger lever arm.
Questions 29–31 refer to the following information:
Two small, identical metal spheres are projected at the same time from the same height by two identical spring guns. Each gun provides the same push on its sphere. However, one sphere is projected vertically upward while the other sphere is projected horizontally. The speed of each projectile as it emerges from the gun is the same. Frictional losses are negligible.
29. How does the speed of the vertically launched sphere compare to the speed of the horizontally launched sphere as they each hit the floor?
(A) It is the same.
(B) It is twice as great.
(C) It is greater but not necessarily twice as great.
(D) It is less.
30. How does the time required for the vertically projected sphere to hit the floor compare with that for the horizontally projected sphere?
(A) It is the same.
(B) It is twice as great.
(C) It is greater but not necessarily twice as great.
(D) It is less.
31. How does the work done by gravity to the vertically launched sphere compare to the work done by gravity to the horizontally launched sphere?
(A) It is the same.
(B) It is twice as great.
(C) It is greater but not necessarily twice as great.
(D) It is less.
Questions 32 and 33 refer to the following information:
A racing car is speeding around a flat, circular track whose radius is 250 m. The car’s speed is a constant 50 m/s, and the car has a mass of 2,000 kg.
32. The centripetal force necessary to keep the car in its circular path is provided by
(A) the engine
(B) the brakes
(C) friction
(D) the steering wheel
33. The magnitude of the car’s centripetal force is equal to
(A) 10 N
(B) 400 N
(C) 4,000 N
(D) 20,000 N
Questions 34 and 35 refer to the following information:
Two small masses, X and Y, are d meters apart. The mass of X is 4 times as great as the mass of Y. Mass X attracts mass Y with a gravitational force of 16 N.
34. The force with which Y attracts X is equal to
(A) 4 N
(B) 16 N
(C) 32 N
(D) 64 N
35. If the distance between X and Y is doubled, then X will attract Y with a force of
(A) 4 N
(B)8 N
(C)16 N
(D)32 N
_____________________________________________________________________
36. A projectile is launched at an angle such that it undergoes projectile motion. In the absence of any air resistance, which of the following statements is correct?
(A) The horizontal velocity increases during the flight.
(B) The horizontal velocity remains constant during the flight.
(C) The horizontal velocity decreases during the flight.
(D) The vertical acceleration changes during the flight.
37. A mass M at the end of a string is spun in a circle of radius R and a constant speed V. Compare the tension in the line when the circle is in a horizontal plane to that of the tensions in at the top and bottom of a vertical plane
38. If you measure the incoming and then outgoing velocities of a baseball as it is hit with a bat, which of the following quantities can be calculated? Assume the mass of the baseball is known.
(A) The average force delivered
(B) The acceleration of the baseball
(C) The time duration of impact
(D) The impulse delivered to the bat
39. An astronaut wakes up inside an accelerating rocket ship in deep space. Using her rubber band of unknown spring constant with attached (unknown) mass, she holds it up against the acceleration and notices the mass stretches the band downwards by X meters. She then pulls it down an additional 5 cm and times the oscillation up and down to be T seconds. The acceleration of her rocket ship in terms of her measurements is
(A) X/T2
(B) KX/m
(C) X(2p/T)2
(D) 0.2/T2
40. A woman standing on a scale in an elevator notices that the scale reads her true weight. From this, she may conclude that
(A) the elevator must be at rest
(B) the elevator must be accelerating precisely at 9.8 m/s2
(C) the elevator must be moving upward
(D) the elevator must not be accelerating
41. A planet has half the mass of Earth and half the radius. Compared with the acceleration due to gravity at the surface of Earth, the acceleration due to gravity at the surface of this planet is
(A) the same
(B) halved
(C) doubled
(D) quadrupled
42. Complete the analogy.
Force is to torque as _______ is to moment of inertia.
(A) momentum
(B) angular momentum
(C) angular acceleration
(D) mass
43. While standing on a moving train, you are suddenly thrown forward as the train stops. This effect can be best explained using Newton’s law of
(A) inertia
(B) acceleration
(C) action and reaction
(D) universal gravity
44. For a falling object to reach terminal velocity (a constant downward speed), the magnitude of the force due to air friction must be
(A) negligible
(B) less than mg
(C) equal to mg
(D) greater than mg
45. An object is in free fall for T seconds. Compare its change in velocity during the first T/2 seconds with its change in velocity during the final T/2 seconds.
(A) They are the same.
(B) They are larger during the first interval.
(C) They are smaller during the first interval by a factor of ½.
(D) They are less than ½ as small during the first interval.
46. Which of the following must be zero if an object is spinning at a constant angular velocity? Select two correct answers.
(A) Net torque
(B) Moment of inertia
(C) Angular momentum
(D) Angular acceleration
47. Which of the following could be used to calculate the time in flight for a horizontally launched projectile on Earth? Ignore friction. Select two correct answers.
(A) The launch speed
(B) The final vertical velocity
(C) The final horizontal velocity
(D) The initial height
48. As an ice skater draws her arms inward during a spin, which of the following remain constant? Select two correct answers.
(A) Her moment of inertia
(B) Her angular momentum
(C) Her angular velocity
(D) The location on the surface of the ice of her center of mass (ignoring any positional changes)
49. A total of three forces, each with a magnitude of 5 N, are exerted on an object with a mass of 15 kg. Which of the following statements are true? Select two correct answers.
(A) The object may be accelerating at 1 m/s2.
(B) The object might not be accelerating.
(C) The object might be accelerating at 2 m/s2.
(D) The sum of the components of the object’s acceleration must add up to the magnitude of its acceleration  .
.
50. A block is put into motion at the top of a hill, giving a velocity at the top of the hill of v1. By the time the block has reached the bottom of the hill, it has doubled its velocity. Which of the following responses are true statements comparing the potential energy stored in the spring initially (Us), the initial gravitational potential energy (Ug), the kinetic energy at the top when the block has v1 (K1), and the kinetic energy at the bottom (K2). Ignore friction in this problem. Select two answers.
(A) K2 = 2K1
(B) Us > Ug
(C) Us + Ug = K2
(D) 3Us = Ug
Section II: Free-Response
TIME: 90 MINUTES
5 QUESTIONS

1. (7 points; ~13 minutes) An elevator ride consists of the following portions.
(a) Initially, the elevator is on the ground floor and quickly speeds up in the upward direction on its way to the top floor.
(b) Most of the trip upward is at a constant velocity.
(c) Suddenly, near the top floor, the elevator comes to a stop just in time for the top floor.
(d) Now the button for the first floor is pressed, and the elevator speeds downward suddenly.
(e) Most of the trip downward is spent at constant velocity.
(f) Suddenly, at the very bottom, the elevator comes to a stop.
(a) Draw a qualitative free-body diagram (showing the relative vector sizes) for each portion of the elevator ride as experienced by a passenger. Next to each, describe how the person would feel (normal, heavier than usual, lighter than usual, etc.).
(b) Explain the difference among the passenger’s mass, gravitational weight, and apparent weight throughout the trip. When (if ever) are these the same, and when (if ever) are they different? Which quantities change during the trip, and which ones do not?
(c) Describe what would happen if, on the way up (during step (B)), the cables were to break. Ignore any frictional effect between the elevator itself and the elevator shaft. Be sure to include a discussion of the relative motion of the elevator car and the passenger. Your answer should include a discussion or sketch of the height above ground, the velocity, and the acceleration experienced by the passenger from the time of the break until the end of the motion.
(d) Sketch the expected behavior of the person’s height as a function of time for situation (c) above. Also sketch the person’s Vy as a function of time as well.
2. (12 points; ~25 minutes) A group of students have been asked to determine the spring constant k of the following setup. They have a known mass and a very smooth tabletop. The only additional equipment they have is metersticks and rulers.
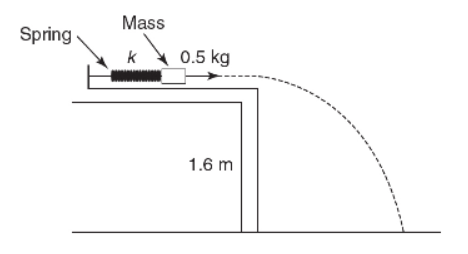
(a) Describe an experimental procedure to determine the spring constant k. You may wish to label the diagram above further to help in your description. Indicate what measurements you would take and how you would take them. Include enough detail so that another student could carry out your procedure.
(b) Determine your independent and dependent variables in order to create a linear plot to determine k. Sketch out the expected graph. Explain your reasoning.
(c) What common sources of error in your procedure might happen during this investigation? What steps could you take to minimize these errors?
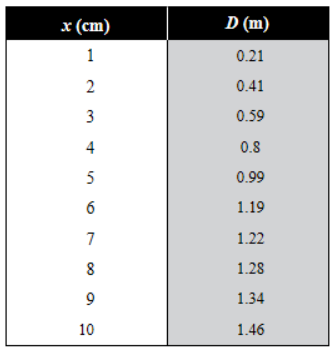
(d) A group of students collected the following data; x is for the spring and D is along the ground. The students found a discontinuity in the behavior of the graph. Graph the data and determine a value for k. Offer a possible explanation for the discontinuity.

3. (12 points; ~25 minutes) Two cars are separated by 25 meters. Both are initially at rest. Then the car in front begins to accelerate uniformly at x meters per second squared. The second car, which is behind, begins to accelerate uniformly at y meters per second squared.
(a) If the second car must catch up with the car in front within 10 seconds, what type of relationship must exist between y and x? Is there a maximum or minimum difference between the two accelerations? Explain using words and equations.
(b) Given that the conditions in question (a) are being met (that is, the second car will catch up to the first within 10 seconds), is there any instant in time that the cars will have the same velocity? Will there be any interval of time over which both cars will have the same average velocity? Support your answers with graphs.
(c) Given that the conditions in question (a) are being met (i.e., the second car will catch up to the first within 10 seconds) and that both cars are continuing to drive with constant velocity for an additional 10 seconds at their instantaneous speeds at the moment the second car has caught up with the first, which car will be ahead and by how much by the end of the trip? Answer this question qualitatively and quantitatively. Specifically determine the minimum and maximum differences in displacement if they can be found.
(d) If both cars are on track to meet the conditions in question (a) (i.e., the second car will catch up to the first within 10 seconds) but both cars are stopped after traveling 50 meters, which one will have expended the most energy? Assume both cars are identical in mass and fuel efficiency. Choose one of the following options, and justify your choice:
_____ The first car expended more energy.
_____ Both cars expended equal energy.
_____ The second car expended more energy.
_____ Which car expended more energy requires more knowledge of exactly when the second car catches up to the first car.
4. (7 points; ~13 minutes) A long-distance, unmanned probe is sent to another planet. To keep it oriented correctly, the probe is given a lot of spin during the early part of the trip. However, when the probe is getting close to its destination, the spin is no longer desired. Two very long cables with mass at the end of each are extended while the probe is still in deep space. Once extended, the cables are released and the probe begins its landing sequence.
(a) Explain qualitatively why the spinning will help keep the probe oriented correctly. Describe the underlying physics concepts using equations and diagrams as needed.
(b) Explain what is accomplished by the action of extending and releasing the cables near the end of the probe’s flight. Describe the underlying physics concepts using equations and diagrams as needed. Do the masses need to be a significant portion of the probe’s mass for this procedure to be effective?
(c)What happens to all of the probe’s linear momentum when it lands on its destination planet? Describe qualitatively in terms of physics principles what happens during the landing.
5. (7 points; ~13 minutes)
(a) A fellow student argues that you cannot use the formula ½gt2 to find the height of a very tall cliff (200 meters or so) when dropping a stone from the top and counting the seconds until impact at the bottom. He says that because of Newton’s law of universal gravity, the acceleration is not constant during the fall. Using equations and calculations, both support and refute his argument. Would his argument have had greater, lesser, or the same power to persuade you if he was talking about a cliff on the Moon? Answer in a clear, coherent paragraph. Use equations to support your reasoning.
(b) Two masses, M and 9M, are separated by a distance of d. At what distance and in what direction from the smaller mass should a third mass be placed such that the net gravitational force on this third mass is zero?




