1. What is the length of a pendulum whose period, at the equator, is 1 s?

(A) 0.15 m
(B) 0.25 m
(C) 0.30 m
(D) 0.45 m

2. On a planet, an astronaut determines the acceleration of gravity by means of a pendulum. She observes that the 1-m-long pendulum has a period of 1.5 s. The acceleration of gravity, in meters per second squared, on the planet is

(A) 7.5
(B) 15.2
(C) 10.2
(D) 17.5

3. When a 0.05-kg mass is attached to a vertical spring, it is observed that the spring stretches 0.03 m. The system is then placed horizontally on a frictionless surface and set into simple harmonic motion. What is the period of the oscillations?

(A) 0.75 s
(B) 0.12 s
(C) 0.35 s
(D) 1.3 s

4. A mass of 0.5 kg is connected to a massless spring with a force constant k of 50 N/m. The system is oscillating on a frictionless, horizontal surface. If the amplitude of the oscillations is 2 cm, the total energy of the system is

(A) 0.01 J
(B) 0.1 J
(C) 0.5 J
(D) 0.3 J

5. A mass of 0.3 kg is connected to a massless spring with a force constant k of 20 N/m. The system oscillates horizontally on a frictionless surface with an amplitude of 4 cm. What is the velocity of the mass when it is 2 cm from its equilibrium position?

(A) 0.28 m/s
(B) 0.08 m/s
(C) 0.52 m/s
(D) 0.15 m/s

6. If the length of a simple pendulum is doubled, its period will

(A) decrease by 2
(B) increase by 2
(C) decrease by
(D) increase by

7. A 2-kg mass is oscillating horizontally on a frictionless surface when attached to a spring. The total energy of the system is observed to be 10 J. If the mass is replaced by a 4-kg mass, but the amplitude of oscillations and the spring remain the same, the total energy of the system will be

(A) 10 J
(B) 5 J
(C) 20 J
(D) 3.3 J

1. A mass M is attached to two springs with force constants k₁ and k₂, respectively. The mass can slide horizontally over a frictionless surface. Two arrangements, (a) and (b), for the mass and springs are shown below.

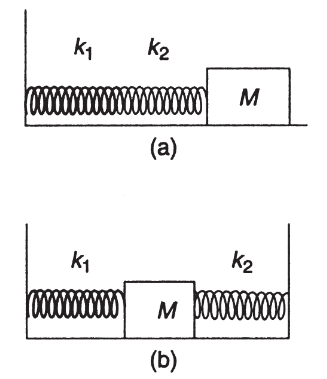
(a) Show that the period of oscillation for situation (a) is given by

(b) Show that the period of oscillation for situation (b) is given by

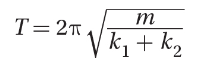
(c) Explain whether the effective spring constant for the system has increased or decreased.

2. A mass M is attached to two light elastic strings both having length ℓ and both made of the same material. The mass is displaced vertically upward by a small displacement Δy such that equal tensions T exist in the two strings, as shown below. The mass is released and begins to oscillate up and down. Assume that the displacement is small enough so that the tensions do not change appreciably. (Ignore gravitational effects.)

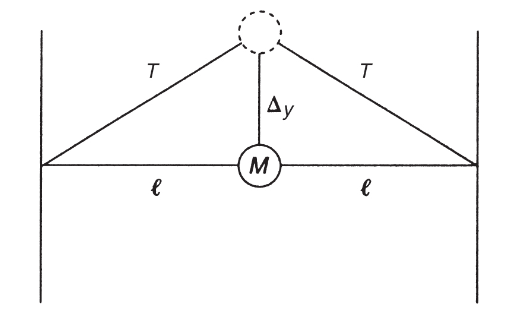
(a) Show that the restoring force on the mass can be given by (for small angles)

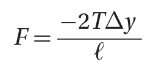
(b) Derive an expression for the frequency of oscillation.

3. Explain why a simple pendulum undergoes only approximately simple harmonic motion.

4. Explain how the mass of an object can be determined in a free-fall orbit using the concept of simple harmonic motion.

5. Both oscillating springs and oscillating pendula can be used as timekeeping devices. Compare the accuracy of both of these devices as timekeeping devices here on Earth versus on the Moon where gravity is 1/6 that of Earth’s.